北方伟业计量集团有限公司
-
登录 |
-
官方微信 |

-
在线支付 |
- 网站地图
- 产品
- 新闻
- 课堂
北方伟业计量集团有限公司









支持向量回归机(Support Vector Regression, SVR)与SVM的主要不同点是寻找的一个最优超平面,不是将两类样本点分离的最远,而是让所有的样本点距离这个最优超平面的总方差最小 。若给定样本数据集{(xi,yi),i=1,2,...,n},其中xi=T,yi∈R,一个回归函数则被建立:

式(5)中,φ(x)为原始特征数据的非线性映射函数,w为权向量,b∈R为阈值。
引入线性不敏感损失函数θ,f(xi)表示预测值,yi为相对应的实际值,|yi−f(xi)|为真实值与预测值之间的差,θ不敏感函数引用的意义在于若|yi−f(xi)|在允许误差范围内,那么f(xi)没有损失,如式(6)所示。引入正则化参数c,式(5)可以转化为式(7)的代价函数:

引入松弛变量ξ1i,ξ2i,可以建立式(8)的目标函数与式(9)的约束条件:
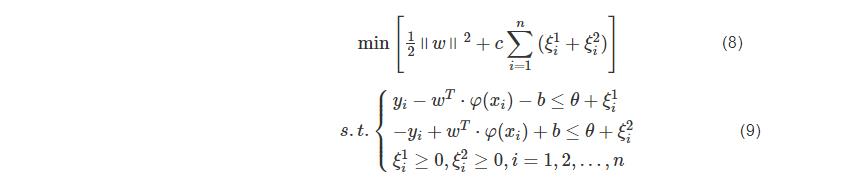
引入拉格朗日函数和核函数K(xi,xj)=φ(xi)φ(xj),可将式(8)和式(9)变换成对偶形式:
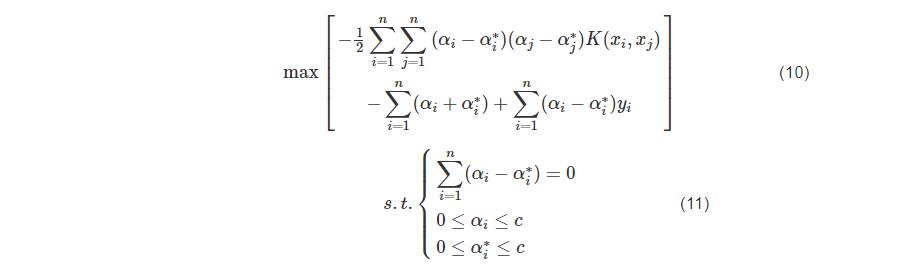
式(10)-(11)中的α为拉格朗日乘子,在KKT(Karush-Kuhn-Tucker)条件下,对最优解α和α∗求解,可以得出:
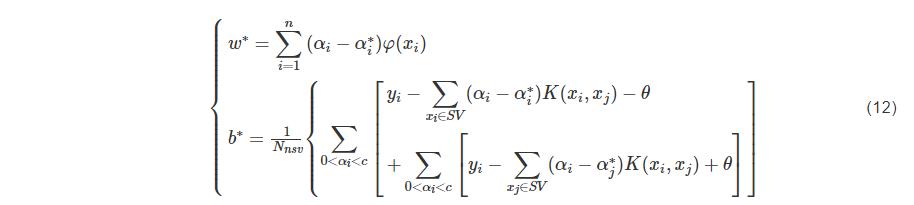
式(12)中Nnsv表示支持向量的个数,计算可得偏置量b∗。综上,最终可得SVR的拟合函数,如式(13):
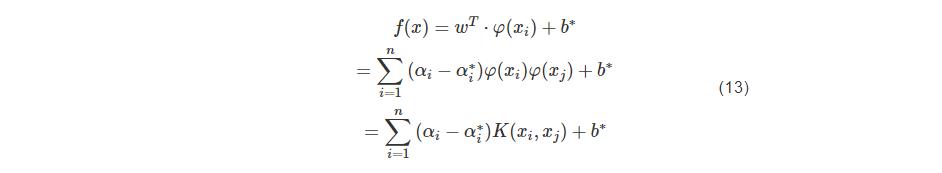
当核函数选择的是式(14)的sigmoid函数时,SVR实现的是一个多层感知器神经网络,对未知变化状况的样本集具有良好的泛化能力,溶解氧的预测值可以表示为式(15):


采集到的数据一般不直接采用,需经过数据的归一化处理。这是因为水质因子指标的范围比较大,不同的数据具有不同的量纲单位,为了消除水质指标彼此之间的量纲影响及保证这些数据之间具有可比性以及提高模型的运行速度和预测精度。本文采用MATLAB R2018a的map-maxmin函数进行归一化处理,如式(23)所示,“apply”模式是将数据指标转化到[-1,1]之间,便于对比预测,而“resver”模式可以将数据反归一化回去。
了解更多> >在选取的样本信息中,水质指标浊度与水温之间的相关系数为0.58>0.5,氨氮与电导率之间的相关系数为0.547>0.5,在99%的置信区间下,具有显著相关性。而互信息值0.7759(浊度)>0.6800(水温),0.7854(电导率)>0.7598(氨氮),因此选取电导率、总磷、浊度、高锰酸钾指数、PH、总氮等作为水质指标中影响溶解氧含量的特征变量。
了解更多> >综上所述,在研究水质指标溶解氧问题时选择的特征变量过少导致建模效果不佳,预测结果不具有代表性,特征变量多可以提供描述问题的更多信息,但数据中会存在无关和弱相关且冗余的特征变量,会降低模型的泛化性能。在对溶解氧预测实践中,PCA-MI特征选择方法选取的特征变量更具有代表性,能更有效的提高模型预测性能。
了解更多> >在解决水质指标溶解氧的预测问题时,将经过PCA和MI组合特征选择的溶解氧数据作为GNIPSO-SVR预测模型的输入,并与BP神经网络、SVR、PSO-SVR等预测模型进行对比分析。各个溶解氧预测模型的总体趋势与实际值都比较吻合,但本文提出的GNIPSO-SVR模型预测DO的曲线更接近实际值的曲线,PSO-SVR模型的预测效果次之,SVR的预测曲线与实际值曲线拟合度最差,尤其是对突变值的拟合情况,各个模型的预测值和实际值的拟合曲线的可视化结果如图4-图7所示。
了解更多> >本文利用主成分分析(PCA)、互信息(MI)、非线性惯性权重递减的粒子群优化算法(GNIPSO)和支持向量回归机(SVR),提出了一种基于高斯函数的非线性权重递减的粒子群算法优化支持向量回归机(GNIPSO-SVR)的预测模型,通过实验证明了GNIPSO算法优化SVR的参数优于标准的PSO算法和惯性权重线性递减的PSO算法。
了解更多> >通话对您免费,请放心接听
温馨提示:
1.手机直接输入,座机前请加区号 如13803766220,010-58103678
2.我们将根据您提供的电话号码,立即回电,请注意接听
3.因为您是被叫方,通话对您免费,请放心接听

登录后才可以评论