基于GNIPSO-SVR的水质预测模型研究（三）

1.3改进的粒子群算法

Eberhart和Kennedy对鸟群的飞行觅食进行观察，通过模拟它们之间的合作和竞争行为提出了基于全局优化的种群并行搜索的粒子群算法(PSO)。假设在D维搜索空间的群体有N个粒子组成，粒子i(i

式(16)中，w为惯性权重，用来平衡PSO算法全局和局部的搜索能力，Vid为粒子的速度，k为当前迭代次数，c1,c2>0分别为粒子的个体学习因子和社会学习因子，r1,r2为0-1的随机数。

惯性权重w表示k-1时刻的速度Vk−1id对k时刻的速度Vkid的影响程度，当惯性权重w<0.8时，粒子群能快速的聚集在一起，易实现局部搜索；当惯性权重w>1.2时，易实现全局搜索。基本PSO的惯性权重是固定的，优化精度较差，只能对部分特定问题有效。为了更好权衡PSO算法全局和局部的搜索能力，提高粒子的搜索性能，Shi和Eberhart提出了线性递减w的粒子群算法，如式(18)所示：

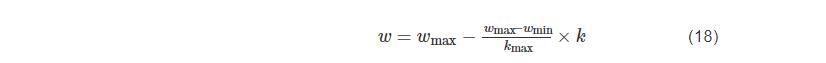
式(18)中wmax为初始权重，wmin为最终权重，kmax为最大迭代次数，k为当前迭代次数。

但PSO算法在解决实际问题的寻优过程中是复杂且非线性变化的，因此惯性权重w需是呈现动态非线性的。而且当PSO算法的w具有随机性，符合正态分布时，能够提高算法的搜索能力[25]。利用高斯函数的分布特性，把相应的参数带入w的变化中，能实现对w的非线性映射[26]。因此，本文结合式(19)的高斯函数，利用式(20)的非线性动态惯性权重不断调整w值，利用式(21)进行位置更新。

式(19)中a,b,c为高斯函数中的实常数；式(20)中wmax为初始权重，wmin为最终权重，k为参数，在文献[中证明了当k=0.2时PSO具有较好的优化性能，因此，本文选取k=0.2，Tmax为最大迭代次数，t为当前迭代次数；式(21)中λ为间的随机数，在粒子每一代搜索时加入随机性，提高种群多样性，提高模型的搜索性能。

2溶解氧组合预测模型的构建

在进行水质指标的研究时，对水质指标进行准确预测可以确保水生环境的污染指标是否保持在允许的范围内，以便采取有效的防控措施。由于水质参数与溶解氧呈现复杂的非线性关系，传统的数据处理技术没有较高的准确性，不能有效地预测溶解氧的含量。而且单一的预测模型通常仅包含水质指标DO的部分信息，通过一定规则组合的模型，包含着更全面的预测信息，提高预测模型的精确度[28]。本文采用PCA的累计方差贡献率来确定特征变量的选取数目，并分析影响因素间的相关性，结合MI值得到对溶解氧影响较大的因素，降低由于变量间的冗余信息带来的误差。

SVR的惩罚函数c可以控制模型训练的误差与复杂度最小化之间的权衡，极小的c值会导致拟合不足的问题，而极大的c值会导致算法对训练数据进行过拟合，内核参数g定义了内核的宽度[9]。由于标准的SVR选择合适的核函数和超参数依赖于试错的过程，是一种耗时的方法，而且非线性SVR模型将非线性输入空间映射到高维特征空间所涉及的固有复杂性，使其行为不容易理解和解释，训练速度较慢。PSO和SVR组合预测方法的引入，可以减少由参数或模型错误识别带来的预测误差。但在实际问题应用中，PSO算法也存在着预测精度低、收敛速度慢等缺点，利用基于高斯函数的非线性惯性权重的粒子群算法(GNIPSO)优化SVR模型的参数，并对溶解氧进行预测，可以实现对无限逼近水质溶解氧真实值生成过程的有效补充。把GNIPSO对SVR的参数(c,g)进行优化，寻找最优的(cbest,gbest)，其预测流程图如图1所示，具体步骤如下：

(1)选择影响溶解氧的关键因素，并考虑空气中的污染物PM2.5、PM10、NO2、SO2、CO、O3，利用主成分分析确定应选择8个关键影响因素，再利用互信息筛选出溶解氧的最优子集特征变量；

(2)数据归一化，把经过特征筛选后的数据采用map-maxmin函数进行归一化处理，并把归一化后的326个样本按照7:3的比例分为训练集(228个)与测试集(98个)作为预测模型的输入与输出；

(3)初始化设置GNIPSO算法的种群大小Psize=30，wmax=0.9，wmin=0.4，学习因子c1与c2，最大迭代次数Tmax，粒子的速度和位置；

(4)把式(22)的均方误差作为适应度函数并计算适应度值，均方误差越小的适应度越佳，yt为第t天的溶解氧含量，yˆt为第t天的DO含量的预测值，N为预测样本数目；

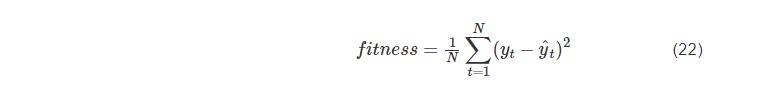
(5)比较粒子即SVR模型的参数(c,g)的适应度值，选择个体的最优值Pi以及群体的最优值Pg，并根据式(16)与式(21)更新每个粒子的速度Vid以及位置Xid，根据式(20)更新w；
 

声明：本文所用图片、文字来源《信息与控制.北大核心CSCD》，版权归原作者所有。如涉及作品内容、版权等问题，请与本网联系删除。

相关链接：水质，溶解氧，粒子